Optimalitätsprinzip von Bellman

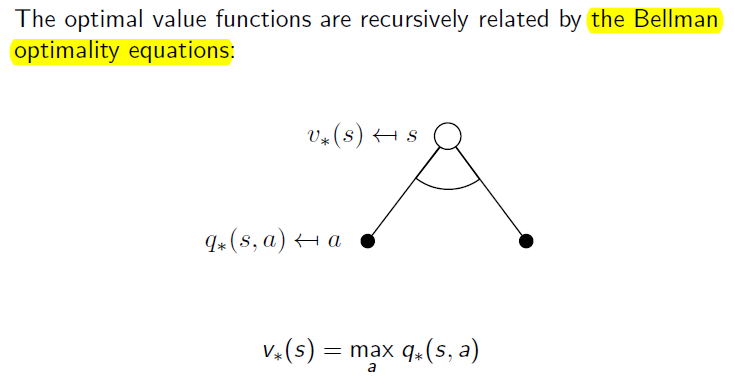
Das Optimalitätsprinzip von Bellman ist ein grundlegendes Prinzip der Optimierung. Es ist nach Richard Bellman benannt und besagt, dass sich bei einigen Optimierungsproblemen jede Optimallösung aus optimalen Teillösungen zusammensetzt. Auf diesem Prinzip basieren Algorithmen der dynamischen Programmierung.

Ein Beispiel ist die Berechnung eines kürzesten Weges in einem Graphen (z. B. einem Straßennetz). Ein kürzester Weg P zwischen den Knoten (Städten) A und B, der durch die Knoten X und Y führt, muss auch zwischen X und Y einen kürzesten Weg zwischen diesen beiden Knoten verwenden. Wäre das nicht der Fall, könnte P verkürzt werden, indem zwischen X und Y ein kürzerer Teilweg verwendet wird, und dann wäre P kein kürzester Weg zwischen A und B gewesen, im Widerspruch zur Annahme. Der Bellman-Ford-Algorithmus zur Berechnung kürzester Wege, der auf dynamischer Programmierung beruht, macht sich dieses Prinzip zunutze. Dargestellt werden solche Graphen in einem Quelle-Senken-Baum.

Definition (Klassisch)

Gemeint ist:

Definition (Formal)

Sei ${\displaystyle h}$ eine Optimierungsfunktion, welche auf Listen arbeitet, dann gilt das Optimalitätsprinzip von Bellman für eine ${\displaystyle k}$-stellige Funktion ${\displaystyle f}$, wenn gilt:

• ${\displaystyle h([f(x_{1},\ldots ,x_{k})|x_{1}\leftarrow z_{1},\ldots ,x_{k}\leftarrow z_{k}])=h([f(x_{1},\ldots ,x_{k})|x_{1}\leftarrow h(z_{1}),\ldots ,x_{k}\leftarrow h(z_{k})])}$
• ${\displaystyle h(z_{1}{ }z_{2})=h(h(z_{1}){ }h(z_{2}))}$

(Giegerich et al., 2002)

${\displaystyle z_{i},1\leq i\leq k}$ sind Listen vom Typ ${\displaystyle A}$. ${\displaystyle h}$ ist vom Typ ${\displaystyle h::[A]->[A]}$. Der ${\displaystyle }$ ist der Listenverknüpfungsoperator und ${\displaystyle [|]}$ ist die Listenbeschreibungs-Notation, wie sie in Haskell definiert sind.

Literatur

• Richard Bellman: Dynamic Programming. Princeton University Press, 1957 (englisch). 
• Thomas L. Morin: Monotonicity and the Principle of Optimality. In: Journal of Mathematical Analysis and Applications. Band 86, 1982, S. 665–674 (englisch). 
• R. Giegerich, C. Meyer, P. Steffen: Towards a Discipline of Dynamic Programming. In: GI Edition - Lecture Notes in Informatics. Bonner Köllen Verlag, 2002, S. 3–44 (englisch, uni-bielefeld.de [PDF; 260 kB]).